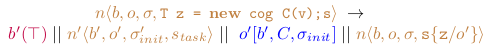Language Tutorial

This tutorial is partially adapted but needs updating to the newest language and tool features

1 Installation of the ABS Eclipse Plugin

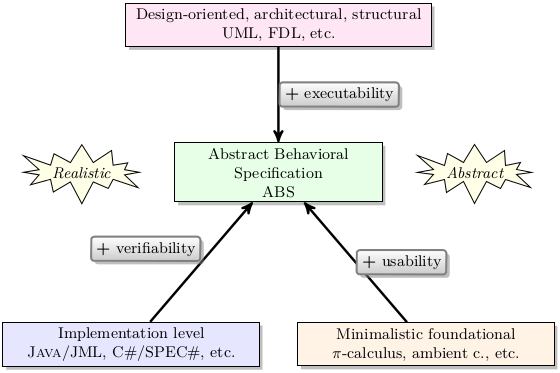
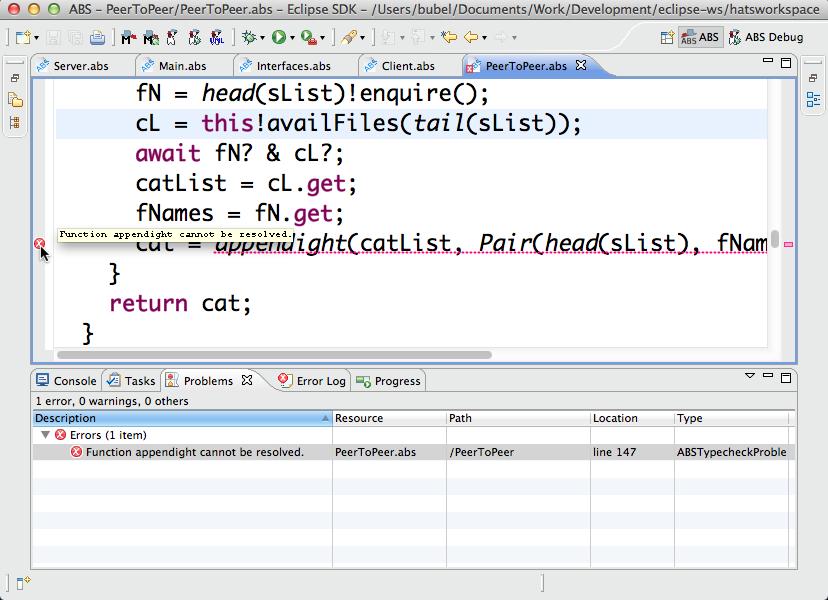
ABS fills a gap in the landscape of software modeling languages. It is situated between architectural, design-oriented, foundational, and implementation-oriented languages [25] For trying out the examples provided in this tutorial you will need the ABS Eclipse plugin. To install it, follow the simple instructions at http://tools.hats-project.eu/eclipseplugin/installation.html. You will need at least Eclipse version 3.6.2 and it is recommended to work with a clean installation. The example project used throughout this tutorial is available as an archive from http://www.hats-project.eu/sites/default/files/TutorialExample.zip. To install, unzip the archive file into a directory /mypath/Account. Then create a new ABS Project and import the directory file contents into Eclipse workspace in the usual way. After opening a few files in the editor you should see a screen similar to the one here:

2 Design Principles of ABS

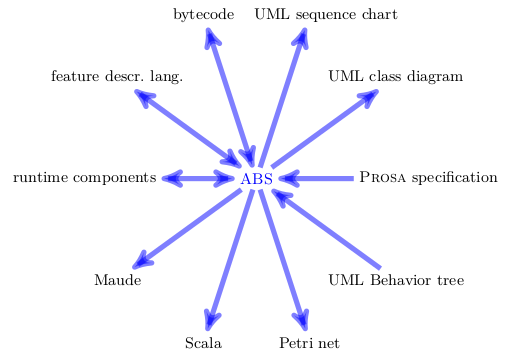
ABS targets software systems that are concurrent, distributed, object-oriented, built from components, and highly reusable. To achieve the latter, we follow the arguably most successful software reuse methodology in practice: software product families or software product lines [35], see also the Product Line Hall of Fame. To this end, ABS supports the modeling of variability in terms of feature models as a first-class language concept. As shown in Sect. 8, ABS thus provides language-based support for product line engineering (PLE). As an abstract language ABS is well suited to model software that is supposed to be deployed in a virtualized environment. To close the gap between design and deployment it is necessary to represent low-level concepts such as system time, memory, latency, or scheduling at the level of abstract models. In ABS this is possible via a flexible and pluggable notation called deployment components. This goes beyond the present, introductory tutorial, but is covered in detail in the chapter by Johnsen in this volume [24]. ABS is not merely a modeling notation, but it arrives with an integrated tool set that helps to automate the software engineering process. Tools are useless, however, unless they ensure predictability of results, interoperability, and usability. A fundamental requirement for the first two criteria is a uniform, formal semantics. But interoperability also involves the capability to connect with other notations than ABS. This is ensured by providing numerous language interfaces from and to ABS as shown in below. These are realized by various import, export, and code generation tools, several of which are discussed below.

Arguably the most important criterion for tools, however, is usability. This tutorial is not the place to embark on a full discussion of what that entails, but it should be indisputable that automation, scalability, and integration are of the utmost importance. To ensure the first two of these qualities, the HATS project adopted as a central principle to develop ABS in tandem with its tool set. This is not merely a historical footnote, but central to an understanding of the trade-offs made in the design of the ABS language. For most specification and programming languages their (automatic) analyzability is considered in hindsight and turns out not to be scalable or even feasible. With ABS, the slogan of design for verifiability that originated in the context of hardware description languages [30], has been systematically applied to a software modeling language. For example, the concurrency model of ABS is designed such that it permits a compositional proof system [3], the reuse principle employed in ABS is chosen in such a way that incremental verification is possible [21], etc. Many formal methods tools focus on analysis, in particular, on verification. Functional verification, model checking, test case generation, and resource estimation are supported by ABS tools as well. Just as important as analytic methods, specifically in a model-based context, are generative ones: ABS is fully executable (albeit in a non-deterministic manner) and supports code generation to Java, Scala, and Maude. In addition, it is possible to learn ABS models from observed behavior [16]. Regarding integration, the tool set around the ABS language is realized as a set of plugins for the popular Eclipse IDE. These plugins realize the ABS

Modeling Perspective (see Fig. 2) and the ABS Debug Perspective (see Fig. 8), which provide the same functionality as their Java counterparts, that is, parsing, syntax highlighting, parse error location, symbol lookup, compilation, building, runtime configurations, interactive debugging, etc. In addition to these standard development tools, however, a number of analysis and generation tools are available as well. Some of these, for example, Java code generation or type inference are illustrated below. An overview of the ABS tool suite is given in [42].

3 Architecture of ABS

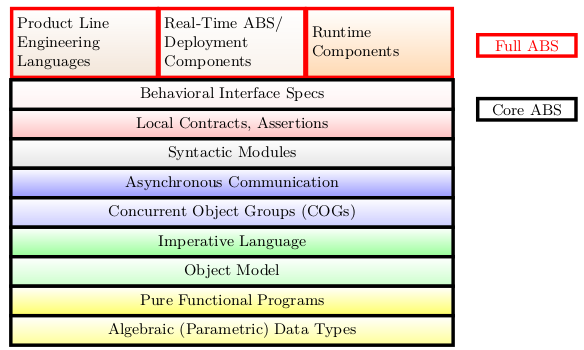
The architecture of ABS has been organized as a stack of clearly separated layers as illustrated in Fig. 4. In the design we strove for

an attractive, easy-to-learn language with a syntax that is familiar to many developers and
to provide maximal separation of concern (orthogonality) among different concepts.

The four bottom layers provide a modern programming language based on a combination of algebraic data types (ADTs), pure functions, and a simple imperative-OO language. The idea is that anyone familiar with either Java and Haskell or with Scala is able to grasp this part of ABS immediately, even though ABS is considerably simpler than any of these languages. The next two layers realize tightly coupled and distributed concurrency, respectively. The concurrency and synchronization constructs are designed in a way to permit a compositional proof theory for functional verification in a program logic [3]. Standard contracts are used for functional specification of sequential programs and behavioral interfaces over sets of histories are used for specifying concurrent programs, see also the paper by Poetzsch-Heffter in this volume [34]. The language layers up to here are often called Core ABS. Above these are orthogonal extensions for product line engineering, deployment components, and runtime components that allow to model mobile code. The latter are not discussed in this volume, but are described in [28]. As mentioned above, ABS is a fully executable language. Nevertheless, abstraction is achieved in a number of ways: first of all, ABS contains only five built-in datatypes—everything else is user-defined. The rationale is that no premature decision on the properties of datatypes is enforced, which helps to create implementation-independent models. Second, functions on datatypes can be underspecified. The modeler has the alternative to return abstract values or to leave case distinctions incomplete. The latter may result in runtime errors, but is nevertheless useful for simulation, test generation or verification scenarios. Third, the scheduling of concurrent tasks as well as the order of queuing messages is non-deterministic. Of course, one might want to give full implementation details at some time. This is possible by refining an ADT into an implemented class or by realizing it in Java via the foreign language interface available in ABS (Sect. 7. Concrete schedulers can be specified via deployment components [24, 32]. Crucially, the abstraction capabilities of ABS allow to specify partial behavior during early design stages, such as feature analysis, without committing to implementation details. This lends support, for example, to rapid prototyping or to the early analysis of consequences of design decisions. ABS has been designed as a compact language. Each layer has no more first-class concepts than are needed to ensure usability (including some syntactic sugar). This does not mean, however, that ABS is a small language: the ABS grammar has considerably more non-terminals than that of Java! The reason is that ABS features several language concepts that are simply not present in Java. In the final analysis, this reflects the ambition of ABS to cover the whole modeling spectrum from feature analysis, deployment mapping, high-level design and down to implementation issues. To show that in spite of this ABS is not unwieldy, but rather easy to use and quite flexible, is the aim of the present tutorial.

4 The Functional Layer

4.1 Algebraic Data Types

The base layer of ABS is a simple language for parametric algebraic data types (ADTs) with a self-explaining syntax. The only predefined datatypes(Foot: There is one more predefined type that is used for synchronization which is explained in Sect. 6.) are Bool,Int, String, Unit and parametric lists as defined below. The type Unit is used as a type for methods without return value and works like Java’s void. All other types are user-defined. We assume that the Eclipse plugin is installed (see Sect. 1.3). To create a new ABS file in an existing ABS project, right click on the project in the explorer and choose New|ABS Module. In the input mask that pops up, specify a file name, for example, CustomerData, and click Finish. This creates a new file named CustomerData.abs in the workspace, which can be edited in the usual way. The running example of this tutorial has a banking theme. Let us create some datatypes related to customers. All type and constructor names must be upper-case.

data Level = Standard | Silver | Gold;
data Customer = Test | Person(Int, Level) | Company(Int);

There are three kind of customers defined by three different type constructors: a test customer, individual customers, and corporate customers. Individual customers are identified by a personal id and possess a status level while corporate customers are identified by their vat number. We can make this more explicit and, at the same, automatically create selector functions for the arguments of each type constructor by the following alternative definition:

data Customer = Test | Person(Int pid, Level) | Company(Int vat);

Assume now that we want to define lists of customers. For this we can use the following built-in parametric list type, which provides a convenient concrete syntax for lists:

data List<T> = Nil | Cons(T, List<T>);
List<Int> l = [1,2,3];

The definition of parametric lists demonstrates that type definitions may be recursive. Let us instantiate parametric lists with Customer and, at the same time, create a type synonym:

type CustomerList = List<Customer>;

Type synonyms do not add new types or functionality, but can greatly enhance readability.

4.2 Functions

The functional layer of ABS consists of a pure first-order functional language with definitions by case distinction and pattern matching. All function names must be lower-case. Let us begin by defining a function that computes the length of a list of customers:

def Int length(CustomerList list) =
    case list {
       Nil => 0 ;
       Cons(n, ls) => 1 + length(ls) ;
       _ => 0 ;
    } ;

Several kinds of patterns are permitted on the left-hand side of case distinctions. In the example above, the first and second cases use a data constructor pattern. In the second case, this contains an unbound variable whose value is extracted and used on the right-hand side. The last case uses an underscore pattern containing an anonymous variable that matches anything. Naturally, it would have been possible to define a parametric version of Int length(List<T> list). This is left as an exercise to the reader. Here is another example illustrating the remaining patterns, that is, the literal pattern and the bound variable pattern:

def Int sign(Int n) =
    case n {
       0 => 0 ;
       n => if (n > 0) then 1 else -1 ;
    } ;

The ABS parser does not attempt to establish whether case distinctions are exhaustive. If no pattern in a case expression matches, a runtime error results. It is up to the modeler to prevent this situation (in the near future, ABS will be equipped with the possibility of failure handling). Similarly, it is perfectly possible to define the following function:

def Int getPid(Customer c) = pid(c);

However, if c has any other type than Person(Int,Level) at runtime, an error will result. We close this section by illustrating a piece of syntactic sugar for associative collection types such as sets, bags, sequences, etc. To construct concrete elements of such datatypes one typically needs to iterate several binary constructors, such as Insert(1,Insert(2,Insert(3,EmptySet))). This is cumbersome. The following idiom defines an n-ary constructor that uses concrete list syntax as its argument. By convention, the constructor should have the same name as the type it is derived from, but in lower-case.

data Set<A> = EmptySet | Insert(A, Set<A>);
def Set<A> set<A>(List<A> l) =
    case l {
       Nil => EmptySet;
       Cons(hd, tl) => Insert(hd, set(tl));
    } ;

Errors are highlighted on the editor line where they occur as well as in the Problems tab of the messages subwindow

Set<Int> s = set[1,2,3];

4.3 Modules

If you tried to type in the previous examples into the ABS Eclipse editor you got parser errors despite the definitions being syntactically correct (similarly as in Fig. 5). This is, because any ABS definition must be contained in exactly one module. ABS is equipped with a simple syntactic module system that is inspired by that of Haskell [33]. To make the examples of the previous section work, simply add a module declaration like this as the first line of the file:

module CustomerData;

Module names must be upper-case and define a syntactic scope until the end of the file or until the next module declaration, whatever comes first. Module names can also be part of qualified type names. Module declarations are followed by export and import directives. The former lists the types, type constructors, and functions that are visible to other modules, the latter lists the entities from other modules that can be used in the current module. With the type definitions of the previous section we might write:

module CustomerData;
export Standard, Customer, Company, getPid;
...
module Test;
import * from CustomerData;
def Customer c1() = Company(2);
def Customer c2() = Person(1,Standard); // erroneous

The module CustomerData exposes three of its constructors and a function while module Test imports anything made available by the former. The definition of c1 is correct, but the definition of c2 gives a parse error about a constructor that cannot be resolved, because Person is not exported. The from clause constitutes an unqualified import. Instead, it is also possible to make qualified imports. For example, we could have written:

import CustomerData.Company, CustomerData.Customer;
def CustomerData.Customer c1() = CustomerData.Company(2);

In this case, however, one must also use qualified type names in the definitions as illustrated above. The ABS compiler knows one predefined module that does not need to be explicitly imported—the ABS standard library ABS.StdLib. It contains a number of standard collection types, such as lists, sets, maps, together with the usual functions defined on them. It also contains some other types and functions that are used often. The standard library module is contained in a file named abslang.abs. To look up the definition of any standard type or function (or any other type or function, for that matter), simply move the cursor over the identifier in question and press F3. For example, pressing F3 over the identifier Cons in the definition of length in the previous section opens a new tab that contains abslang.abs and jumps to the line that contains the definition of the constructor Cons. This lookup functionality is, of course, well-known to users of the Eclipse IDE.

4.4 Abstract Data Types

The module system allows to define abstract data types by hiding the type constructors. This implies that only functions can be used to access data elements. Their explicit representation is hidden. Of course, one then needs to supply suitable constructor functions, otherwise, no new elements can be created at all. In the example of the previous section we might decide to expose only the types and constructor functions as follows:

module CustomerData;
export Customer, Level, createCustomer, createLevel;
def Customer createCustomer(Int id, String kind) = ... ;
def Level createLevel() = ... ;

We leave it as an exercise to write a suitable definition of createCustomer. As usual, the advantage of using abstract data types is that one can replace the definition of types without the need to change any client code.

5 The OO-Imperative Layer

5.1 The Object Model

ABS follows a strict programming to interfaces discipline [17]. This means that the only declaration types of objects are interface types. Consequentially, ABS classes do not give rise to type names. Apart from that, interface declarations are pretty standard and follow a Java-like syntax. They simply consist of a number of method signatures. Static fields are not permitted,(Foot: And neither are static classes and objects. Instead of static elements the ABS modeler should consider to use ADTs and functions.) but subinterfaces, even multiple subinterfaces, are permitted. Let us give an example that models the Customer type from previous sections in an object-oriented fashion:

module CustomerIF;
export Customer;
import Level, createLevel from CustomerData;
interface Customer { Int getId(); }
interface IndvCustomer extends Customer {}
interface CorpCustomer extends Customer { Level getLevel(); }

As can be seen, interfaces (and also classes) can be exported. In fact, this is necessary, if anyone outside their modules is to use them. It is possible to mix object and data types: data types may occur anywhere within classes and interfaces as long as they are well-typed. Less obviously, reference types may also occur inside algebraic data types. As seen earlier, it is perfectly possible to declare the following type:

type CustomerList = List<Customer>;

Keep in mind, though, that it is not allowed to call methods in function definitions. The reason is that method calls might have side effects. It was mentioned already that classes do not provide type names. They are only used for object construction. As a consequence, in ABS it is always possible to decide when a class and when an interface name is expected. Therefore, interfaces and classes may have the same name. We do not recommend this, however, because it dilutes the programming to interfaces discipline. It is suggested to use a base name for the interface and derive class names by appending “Impl” or similar. A class may implement multiple interfaces. Class constructors are not declared explicitly, instead, class declarations are equipped with parameter declarations that implicitly define corresponding fields and a constructor. Class definitions then consist of field declarations, followed by an initialization block and method implementations. Any of these elements may be missing. Hence, we can continue the example as follows:

class CorpIndvCustomerImpl(Int id) implements IndvCustomer, CorpCustomer {
    Level lv = createLevel();
    // no initialization block
    Level getLevel() { return lv; }
    Int getId() { return id; }
}

Here, the id field is modeled as a class parameter, because it is not possible to give a reasonable default value, which is otherwise required, because fields that have no reference type must be initialized. Reference type fields are initialized with null. In contrast to functions, method names need not (and cannot) be exported by modules. It is sufficient to get hold of an object in order to obtain access to the methods that are defined in its type. The most striking difference between ABS and mainstream OO languages is that in ABS there is no class inheritance and, therefore, also no code inheritance. So, how do we achieve code reuse? In ABS we decided to disentangle data design and functionality from the modeling of code variability. For the former, we use functions and objects (without code inheritance), whereas for the latter we use a layer on top of the core ABS language that permits to connect directly with feature models. This layer is discussed in Sect. 8. In a concurrent setting (see Sect. 6) one typically wants some objects to start their activity immediately after initialization. To achieve this in ABS, one can define a Unit run() method, which implicitly declares a class as active and lets objects execute the code in the body of the run method after initialization. Classes without a run() method are called passive and their objects react only to incoming calls.

5.2 The Imperative Layer

ABS has standard statements for sequential composition, assignment, while-loops, conditionals, synchronous method calls, and method return. To illustrate all of these, one can look at the implementation of method findCustomer( CustomerList) in class CorpIndvCustomerImpl (don’t forget to add it to the implemented interfaces as well to render it visible!).

Customer findCustomer(CustomerList cl) {
    Customer result;
    Int i = 0;
    while (i<length(cl)) {
        Customer curCust = nth(cl,i);
        Int curId = curCust.getId();
        if (id==curId) {result = curCust;}
    }
    return result;
}

In addition to the various constructs, we can illustrate several ABS-specific restrictions: it is necessary that the final statement in the method body is a return statement with the correct type. A typical ABS idiom is, therefore, to declare a local result variable. Neither for-loops nor breaks from loops are supported at the moment. To avoid going through the remaining list after the element has been found, one would need to add and test for a Bool found variable. Complex expressions are not allowed at the moment in tests of conditionals or loops. The workaround, as shown here, is to declare a local variable that holds an intermediate result. While these restrictions can be slightly annoying they hardly matter very much. It is likely that some of them will be lifted in the future, once it is better known what modelers wish. A more fundamental restriction concerns the usage of fields in assignment statements: assignments to fields and field lookups are only possible for the current object. Given a field f, an assignment of the form x = f; is always implicitly qualified as x = this.f; and an assignment of the form f = exp; is always implicitly qualified as this.f = exp;. This implies that fields in ABS are object private. They cannot be directly seen or be modified by other objects, not even by objects from the same class (as is possible even for private fields in Java). In other words, ABS enforces strong encapsulation of objects: it is only possible to view or change the state of another object via getter- and setter-methods. For example, it is not possible to change the second line in the body of the while-loop of findCustomer(CustomerList) as follows:

Int curId = curCust.id;

The designers of ABS consider object encapsulation not as a restriction, but as a virtue: it makes all cross references between objects syntactically explicit. This avoids errors that can be hard to find. In addition it makes static analysis much more efficient, because any cross reference and possible side effect to a different object can be associated with a unique method contract. For the practicing ABS modeler object encapsulation is greatly alleviated by the method completion feature of the Eclipse editor: if one types the beginning of the example above “Int curId = curCust.”, then a pop-up menu will offer a selection of all methods that are known for objects of type Customer, the required getter-method getId() among them. If a suitable method is not found, then the modeler can take this as a hint that it needs to be implemented or added to the interface. ABS is a block-structured language. Blocks are delimited by curly braces (no semicolon afterward) and may appear at four different places in a program:

as a way to group several statements and provide a scope for local variables–blocks are necessary for bodies of loops and conditionals that have more than one statement;
as method bodies;
as the (optional) class initialization block, between field and method declarations;
as an (optional) implicit “main” method at end of a module.

The last usage serves as an entry point for execution of ABS programs. At least one main block in one module is necessary for executing an ABS project, otherwise it is not clear which objects are to be created and executed. Any module that has a main block is selectable as an execution target via the Eclipse Run Configurations ... dialog or simply by right clicking on the desired module in the explorer and selection of Run As. We might complete the example by specifying the following main block for module CustomerIF:

{
    Customer c = new CorpIndvCustomerImpl(17); // create some customers
    Customer d = new CorpIndvCustomerImpl(16);
    CustomerList l = Cons(c,Cons(d,Nil)); // create list of customers
    Customer e = c.findCustomer(l); // we should find c in l
}

This code illustrates at the same time the usage of the new statement, which works as in Java. As usual in Eclipse, pressing the F4 key displays the type hierarchy pertaining to a class or interface name at the cursor position.

6 The Concurrency Layers

6.1 Background

One of the most distinctive features of ABS is its concurrency model. If we look at commercial programming languages such as C, C++, or Java, one can observe that, despite intense efforts in the last decade, none of them has a fully formalized concurrency model. Even though there are promising efforts towards a formal concurrency model of Java [5], the details are so complex that they are likely to compromise usability of any resulting system. The reason is that current industrial programming languages have a very low-level concurrency model and do not natively support distributed computation. This has practical consequences, such as burdening the programmer with, for example, prevention of data races. A more fundamental problem is the impossibility to design a compositional proof system for such languages. By compositionality we mean that one can specify and verify the behavior of a single method in isolation from the rest of the system. This is a prerequisite for being able to deduce global behavior from the composition of local behavior. In a setting, where concurrent objects can arbitrarily cross-reference each other, this is hardly possible.

Arbitrarily complex, global invariants, might be needed to describe behavior. One approach to tackle the problem is to impose structure on concurrent objects and to make their dependencies syntactically explicit. In the realm of Java, JCoBox [39] is a suitable framework. It has been simplified and renamed into Concurrent Object Group (COG) in the context of ABS. COGs constitute the lower tier of the ABS concurrency model and are intended for closely cooperating concurrent tasks. A second shortcoming of mainstream programming languages is the lack of support for distributed computation, that is, asynchronous communication among nodes that do not share memory. This form of concurrency has been abstracted into the Actor model [23] and is realized with first-class support in recent languages such as Scala. ABS implements a version of Actor-based distributed computation where COGs form the primitive units of distribution. This constitutes the upper tier of the ABS concurrency model. Its main ideas are derived from the modeling language Creol [26].

6.2 Component Object Groups

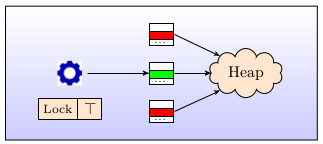
An ABS Concurrent Object Group (COG) is a collection of tasks with shared memory and processor. This means that exactly one task is active at any given time and tasks can cross-reference each other. The situation can be visualized as in Fig. 6. Within a COG, synchronous as well as asynchronous method calls are permitted. For the former, we use the standard syntax target.method(arg1,arg2,...). Synchronous method calls within COGs represent sequential execution of code, that is, they block the caller and execute the code of the target until control is returned. Asynchronous method calls use the syntax target!method(arg1,arg2,...) and they cause the creation of a new task that is to execute the code of the target. Unlike in synchronous calls, execution of the code of the caller continues. The main point to understand about COGs is that multitasking is not preemptive (decided by a scheduler). Rather it is an explicit decision of the ABS modeler when control is transferred to another task. To this end, ABS provides scheduling statements that allow cooperative multitasking. In between the explicit scheduling points, only one task is active, signified by the (single) lock of a COG being set to &#8868. As a consequence, data races between synchronization points simply cannot happen, which was an important design goal of ABS.

6.3 Scheduling and Synchronization

So, how are scheduling points specified in ABS? It is here that we encounter a second, central concurrency principle of ABS: communication and synchronization are decoupled. This is done via future types [12]. For any ABS type T a legal type name is Fut<T> and one can assign to it the result of any asynchronous method call with return type T. A variable declared with type Fut<T> serves as a reference to the future result of an asynchronous call and allows to retrieve it once it will have been computed. For example, the final line of the example on p. 15 can be rewritten to:

Fut<Customer> e = c!findCustomer(l);
// do something else ...

Now the call creates a new task in the current COG and declares e as a future reference to its final result. The following code is executed immediately. The future mechanism allows to dispatch asynchronous calls, continue with the execution, and then synchronize on the result, whenever it is needed. Synchronization is achieved by the command await g, where g is a polling guard. A guard is a conjunction of either side-effect free boolean expressions or future guards of the form f?. In the latter, f is a variable that has a future type. If the result to which f? is a reference is ready and available, then the expression evaluates to true. When the guard of an await statement evaluates to true, the computation simply continues. If, however, a guard is not true, then the current task releases the lock of its COG and gives another task in that COG the chance to continue. When later the task is scheduled gain, the guard is re-evaluated, and so on, until it finally becomes true. We call this a conditional scheduling point or conditional release point. To continue the previous example we could write:

await e?;

If the asynchronous call to findCustomer(l) has finished, then execution simply continues. Otherwise, the lock of the current COG is set to ⊥ and the processor is free to proceed with another task. For efficiency reasons ABS allows only monotonic guards and only conjunctive composition. Once the result from an asynchronous call is available, it can be retrieved with a get-expression that has a future variable as its argument. In the example this may look as follows:

Customer f = e.get;

In summary, the following programming idiom for asynchronous calls and retrieving their results is common in ABS:

Fut<T> v = o!m(e); ... ; await v?; r = v.get;

ABS does not attempt to check that each get expression is guarded by an await statement. So what happens when the result of an asynchronous call is not ready when get is executed? The answer is that the execution of the COG blocks. The difference between suspension and blocking is that in the latter case no task in same COG can continue until the blocking future is resolved. Sometimes it is convenient to create an unconditional scheduling point, for example, to insert release points into long running sequential tasks. The syntax for unconditional scheduling statements in ABS is “suspend;”.

6.4 Object and COG Creation

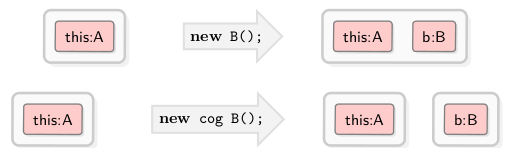
In the previous section we discussed the fundamental concurrency model of ABS, which is based on COGs. Whenever we create an object with the new statement, it is by default created in the same COG as the current task (see upper part of Fig. 7). This is not adequate for modeling distributed computing, where each node has its own computing resources (processor) and nodes are loosely coupled. In an ABS model of a distributed scenario we associate one COG with each node. New COGs are implicitly created when specifying the cog keyword at object creation (see lower part of Fig. 7): this creates a new COG and places the new object inside it. At the moment, COGs are not first-class objects in ABS and are accessible only implicitly through their objects.(Foot: There is an extension for ABS runtime objects that allows explicit and dynamic grouping of COGs [28].) As a consequence, it is not possible to re-enter via recursive calls into the same execution thread. This is the reason why a simple binary lock for each COG is sufficient. Let us extend our running example with an Account class and COG creation:

module Account;
interface Account {
    Int getAid();
    Int deposit(Int x);
    Int withdraw(Int x);
}

class AccountImpl(Int aid, Int balance, Customer owner)
implements Account { ... }

{
    [Near] Customer c = new CorpIndvCustomerImpl(3);
    [Far] Account a = new cog AccountImpl(1,0,c);
    Fut<Int> dep = a!deposit(17);
    Fut<Int> with = a!withdraw(17);
    await dep? & with?;
    Int x = dep.get;
    Int y = with.get;
    Int net = x + y;
}

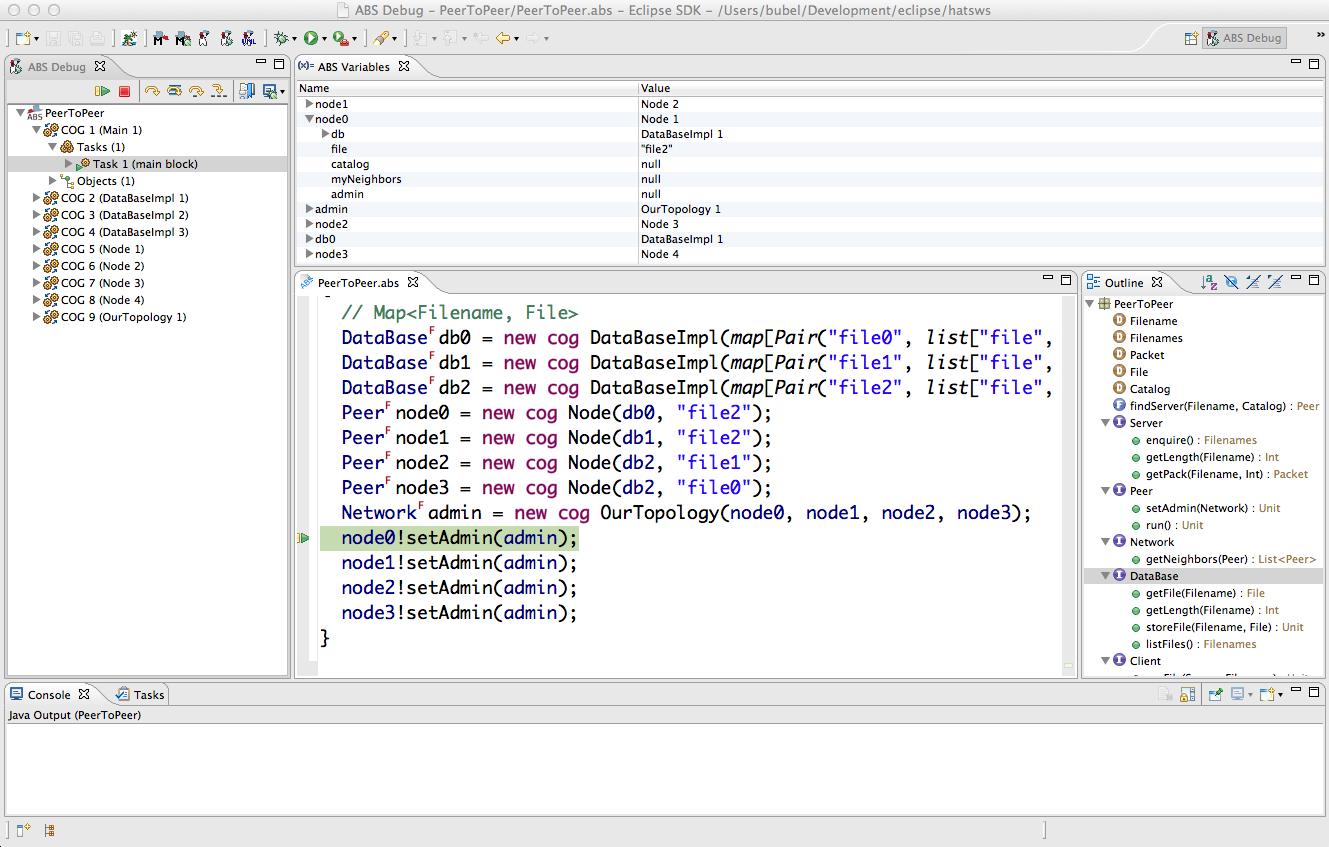
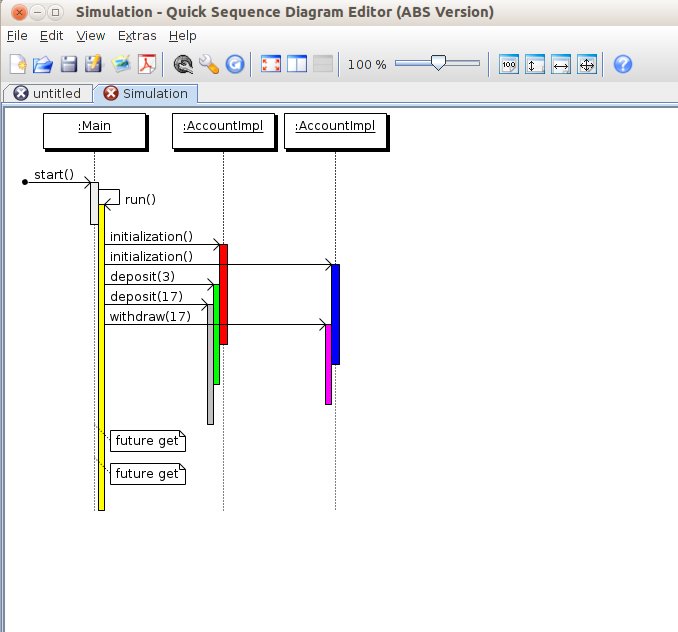
We create an account objects in a different COG from the current one. Note that there is no sharing of objects between COGs, so that the variable c provides no alias to the object parameter c in the constructor AccountImpl(1,0,c). The tasks resulting from the two asynchronous calls will be executed on the same node, which is different from the current one. A conjunctive guard ensures that the retrieval of the results is safe. It is possible to visualize the execution of ABS code in two ways. To start the graphical ABS Debugger, simply right click on the file with the Account module in the explorer and select Run As|ABS Java Backend (Debug). This will automatically switch to the ABS Debug Perspective (see Fig. 8) and start the Eclipse debugger.

All the usual features of a graphical debugger are available: navigation, breakpoints, state inspection, etc. If instead, the backend Run As|ABS Java Backend (Debug with Sequence Diagram) is chosen, then in addition a UML sequence diagram that has a lifeline for each created COG is created and dynamically updated after each debugger step, see Fig. 9. Synchronous method calls to targets not in the current COG make no sense and are forbidden. For example, if we replace one of the asynchronous calls above with a.deposit(17), a runtime error results. One possibility to avoid this is to annotate declarations with one of the types Near or Far, as shown above. This tells the compiler that, for example, a is in a different COG and cannot be the target of a synchronous call. Obviously, it is tedious to annotate all declarations; moreover, the annotations tend to clutter the models. To address this problem, ABS implements a far/near analysis, which automatically infers a safely approximated (in case of doubt, use “far”) location type [41]. The inferred types are displayed in the Eclipse editor as superscripts (“N” for near, “F” for far) above the declared types. All annotations in the example can be inferred automatically: simply delete the annotations to see it. It is also possible to annotate a declaration with Somewhere, which overrides the type inference mechanism and tells the compiler not to make any assumptions. Default is the annotation Infer, but this can be changed in the ABS project properties. It is entirely possible that execution of an ABS model results in a deadlock during runtime, as is exemplified by the model in Fig. 10. Objects c, e and d are in different COGs, say cog_c and cog_d . The task that executes m1 is in cog_c while the task executing m2 is put into the second COG cog_d . During this execution m3 is called on e, which is located in the first COG cog_c . For m3 to proceed it needs to obtain the lock of cog_c , but this is not possible, because m1 still waits for the result of m2. Hence, neither COG can progress. Deadlocks are very difficult to avoid in general. Deadlock-free concurrent languages tend to be too restrictive to be usable and, unlike data race-freeness, are not a practical option.

class C {
    C m1(C b, C c) { Fut<C> r = b!m2(c); return r.get; }
    C m2(C c) { Fut<C> r = c!m3(); return r.get; }
    C m3() { return new C(); }
}
{
    C c = new C(); C d = new cog C(); C e = new C();
    c!m1(d,e);
}

Fig. 10. Example for deadlock in ABS

In ABS many deadlocks can be avoided by supplying enough release points. In the example above it is sufficient to guard one of the get expressions. In addition, there is an automatic deadlock analysis for ABS [18] that is currently being implemented.

6.5 Formal Semantics of Concurrent ABS

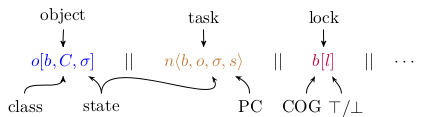
The ABS language has a mathematically rigorous, SOS-style semantics [13, 25]. This tutorial introduction is not the place go into the details, but we sketch the main ideas. The central issue is to give an appropriate structure to the terms that represent ABS runtime configurations. They are collections over the following items:

COGs are identified simply by a name b for their lock whose value can be either ⊤ or ⊥. Objects have a name o, need to have a reference to their COG b, to their class C, and they also have a local state σ that holds the current field values. Tasks have a name n, a reference to their COG b and to the object o whose code they are executing. They also have a state σ withe values of local variables and a program counter s that gives the next executable instruction. Task names n also double as futures, because they contain exactly the required information. A runtime configuration may consist of any number of the above items. The operational semantics of ABS is given by rewrite rules that match the next executable statement of a task (and thereby also the current COG and object). A typical example is the rewrite rule that realizes creation of a new COG:

where:

$b’, o’, n’$ new;
$\overline{T f}; s’$ init block of class $C$ and $\sigma’_{init}$ binds constructor parameters $v’$;
$\sigma’_{init} = \overline{T f}$;
$s_{task} = s’\{\mathbf{this}\, / o’;\mathbf{suspend}\}$.

The rule matches a new cog statement in task $n$, COG $b$, current object $o$, and subsequent statements s. First we need to create a new COG with a fresh name $b’$ and a new object $o’$ of class $C$. The new COG starts immediately to execute the initialization code of its class $C$ in a new task $n’$, therefore, the lock of $b’$ is set to ⊤. Note that the current object this must be instantiated now to the actual object $o’$. After initialization, execution is suspended. The original task $n$ immediately continues to execute the remaining code s as there is no release point here. The value of the object reference z is replaced with the new object $o’$.

7 Extensions

7.1 Pluggable Type System

All declarations (fields, methods, classes, interfaces) in ABS can carry annotations. These are simply expressions that are enclosed in square brackets. The location type system in Sect. 6.4 provided examples. Other annotations can be logical expressions that are used as assertions, contracts, or invariants during verification or runtime assertion checking. This goes beyond this tutorial. The location types are a so-called pluggable type system. Such type systems can be realized easily in ABS via meta annotations. The special annotation [TypeAnnotation] declares the data type definition immediately following it to be a definition for type annotations and makes the parser aware of it. For example, the location type system is declared as follows:

[TypeAnnotation]
data LocationType = Far | Near | Somewhere | Infer;
// usage
[LocationType: Near] T n;

7.2 Foreign Language Interface

As a modeling language ABS does not contain mechanisms for I/O, because these are typically implementation-dependent. Of course, one often would like to have some output from the execution of an ABS model. This is possible with a general foreign language interface (FLI) mechanism that not only can be used to implement I/O for ABS, but to connect ABS models with legacy code in implementation languages in general. At the moment, the ABS FLI is realized for the Java language. An ABS class that is to be implemented in Java needs three ingredients:

import of helper functions and classes from the module ABS.FLI;
declaration as being foreign by the annotation [Foreign];
default ABS implementations of all interface methods.

A simple example can look as follows:

import * from ABS.FLI;
interface Hello { String hello(String msg); }
[Foreign]
class HelloImpl implements Hello {
    String hello(String msg) { return "default implementation"; }
}
{
    Hello h = new HelloImpl();
    h.hello("Hi there");
}

The default implementation is used for simulation of ABS code without Java. It is now possible to implement a Java version of the HelloImpl class in a Java project and to connect that project with ABS. The details of how this is done are explained at the HATS tools site. Basically, one extends the Java class HelloImpl_c that was generated by the ABS Java backend with a new implementation of the Java method hello(String). By convention, the Java methods carry the prefix fli.

import abs.backend.java.lib.types.ABSString;
import abs.backend.java.lib.runtime.FLIHelper;
import Test.HelloImpl_c;
public class HelloImpl_fli extends HelloImpl_c {
   @Override
   public ABSString fli_hello(ABSString msg) {
      FLIHelper.println("I got "+msg.getString()+" from ABS");
      return ABSString.fromString("Hello ABS, this is Java");
   }
}

On the Java side any Java construct can be used. ABS provides a Java package abs.backend.java.lib.types containing declarations of the built-in ABS types usable in Java such as ABSString. Execution of the ABS main block above will now cause the Java output “I got Hi there from ABS” to be printed on the system console.

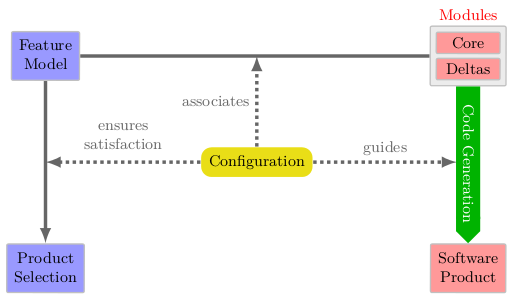
8 Product Line Modeling with ABS

8.1 Product Line Engineering

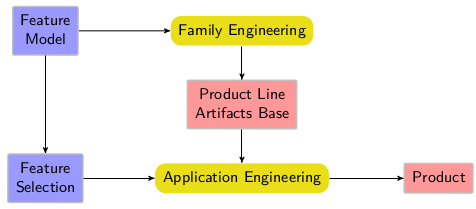
One of the aims of ABS is to provide a uniform and formal framework for product line engineering (PLE) [35], a practically highly successful software reuse methodology. In PLE one distinguishes two separate development phases (see Fig. 11). During family engineering one attempts to distill the commonality among different products into a set of reusable artifacts. At the same time, the variability of the product line is carefully planned. This is typically done in a feature-driven manner, and the relation of features, as well as constraints in their combination is documented in a feature model with the help of feature description languages [40]. In the application engineering phase, individual products are being built by selecting features and by combining the artifacts that implement them in a suitable way. One drawback of current practice in PLE is that feature description languages make no formal connection between features and their implementation. This renders products assembly ad hoc and error-prone. That issue is addressed in ABS with language extensions for modeling of features, for connecting features to their realization, as well as for feature selection and product specification [10]. In this section we introduce the PLE extensions of ABS. A fuller discussion of various approaches to achieve greater flexibility in object-oriented modeling is contained in the chapter by Clarke in this volume [8]. If one wants to maintain a connection between features and code, then the central issue are the mechanisms being used to compose the code corresponding to new features with the existing code. In current practice, this is often done by “glue code” written in scripting languages. ABS has the ambition that models can be statically analyzed. This means that the feature composition mechanism must be well-structured and represent a suitable match for the analysis methods used in ABS [14].

Such a mechanism is delta-oriented programming (DOP) [36, 38], because it allows to modify object-oriented code in a structured manner at the granularity of fields and methods, which is adequate for the contract-based specification approach in ABS [21]. To summarize, the ABS-extensions used to model product lines consist of four elements [9, 10], which we describe now in turn:

A feature description language
A language for deltas that modify ABS models
A configuration language connecting features with the deltas that realize them
A language for product configuration

8.2 Feature Description

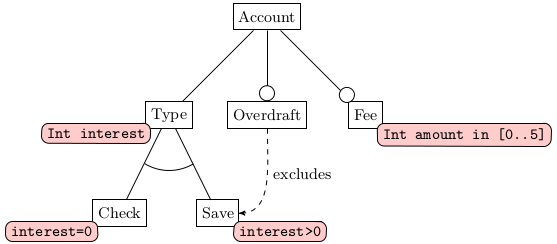
Modern software development processes, notably agile processes and PLE, tend to be feature-driven. A number of mature and useful formalisms for feature description have been developed in the last decade. For ABS we use a slight modification of the textual variability language (TVL) [11], which has the advantage of having a formal semantics and a textual representation. The feature description language used in ABS is called μTVL and differs from TVL in that (i) attribute types that are not needed are omitted and (ii) the possibility to have multiple root features. These are useful to model orthogonal variability in product lines. Let us build a product line based on the Account interface from Sect. 6.4. Assume we want to distinguish between checking and saving accounts. The latter may pay interest, whereas the former usually don’t. Optionally, a checking account (but not a saving account) may permit an overdraft or incur fees for transactions. A graphical representation of the Account feature model is in Fig. 12. The textual rendering in μTVL looks as follows:

root Account {
   group allof {
      Type {
         group oneof {
            Check {ifin: Type.i == 0;},
            Save {ifin: Type.i > 0;
            exclude: Overdraft;}
         }
         Int i; // interest rate
      },
      opt Fee {Int amount in [0..5];},
      opt Overdraft
   }
}

In μTVL one represents each subhierarchy in the feature tree by a group of features, which can be further qualified as inclusive (allof) or alternative (oneof). Within a group there is a comma-separated list of feature declarations. Each feature declaration may be optional (opt) and have restrictions (ifin:), exclusions (exclude:), or requirements (include:). Feature parameters are declared after the declaration of a subhierarchy. A feature model appears in a separate file with extension .abs. The Eclipse editor supports syntax and parse error highlighting. There can be several feature files with feature declarations. These are interpreted as orthogonal feature hierarchies that are all part of the same feature model. The semantics of feature models is straightforward by translation into a boolean/integer constraint formula, see [10, 11]. For example, the feature model above is characterized by the following formula: 0 ≤ Account ≤ 1 ∧ Type → Account ∧ Overdraft† → Account ∧ Fee† → Account ∧ Type + Fee† + Overdraft† = 3 ∧ 0 ≤ Type ≤ 1 ∧ Check → Type ∧ Save → Type ∧ Save → ¬Overdraft ∧ Check + Save = 1 ∧ 0 ≤ Check ≤ 1 ∧ 0 ≤ Save ≤ 1 ∧ 0 ≤ Fee† ≤ 1 ∧ 0 ≤ Overdraft† ≤ 1 ∧ Fee → Fee† ∧ Overdraft → Overdraft† ∧ 0 ≤ Save ≤ 1 ∧ 0 ≤ Check ≤ 1 ∧ Fee → (Fee.amount >= 0 ∧ Fee.amount <= 5) ∧ Check → (Type.i = 0) ∧ Save → (Type.i > 0). It is easy to check validity of a given feature selection for a feature model F : for any selected feature f and parameter value p := v one simply adds f = 1 ∧ p = v to the semantics of F and checks for satisfiability with a constraint solver. The constraint solver of ABS can:

find all possible solutions for a given feature model and
check whether a feature selection is a solution of a feature model.

The latter check is performed implicitly in the ABS Eclipse plugin, whenever the user requests to build a product based on a specific feature selection (see Sect. 8.5).

8.3 Delta Modeling

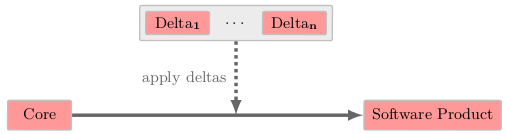
As mentioned above, the realization of features in ABS is done with delta modules (or deltas, for short), a variant of delta-oriented programming (DOP). This constitutes the main reuse principle of ABS and replaces other mechanisms such as code inheritance, traits, or mixins. In delta modeling we assume that one outcome of the family engineering phase (see Fig. 11) is a core or base product with minimal functionality. Product variants with additional features are obtained from it by applying one or more deltas that realize the desired features, as illustrated in Fig. 13. In ABS, deltas have the following capabilities:

Delta modules may add, remove or modify classes and interfaces
Permitted class modifications are:
- adding and removal of fields
- adding, removal and modification of methods
- extending the list of implemented interfaces

The actual reuse mechanism is located in the modification of methods: the description of a method modification in a delta can access the most recent incarnation of that method in a previous delta by the statement original(...);. This will cause the compiler to insert the body of the referred method at the time when the deltas are applied. The signature of original() must be identical to the one of the modified method. The compiler checks the applicability of deltas and ensures well-typedness of the resulting code. It is because of this reuse mechanism that once can say that the granularity of delta application is at the level of methods. There is a certain analogy between original() in DOP and super()-calls in OO languages with code inheritance. The crucial difference is that original() references are resolved at compile time (product build time), while super()-calls occur at runtime. As a consequence, there is a runtime penalty for the latter. Assume we have the following implementation of the withdraw(Int) method of the Account interface, which ensures that we cannot withdraw more than the current balance:

class AccountImpl(Int aid, Int balance, Customer owner)
implements Account {
   Int withdraw(Int x) {
      if (balance - x >= 0) { balance = balance - x; }
      return balance;
   }
}

Now we would like to create a delta module that realizes the feature Fee. We need to modify withdraw(Int), which can be achieved by the following delta:

delta DFee(Int fee); // Implements feature Fee
uses Account;
modifies class AccountImpl {
   modifies Int withdraw(Int x) {
      Int result = x;
      if (x>=fee) result = original(x+fee);
      return result;
   }
}

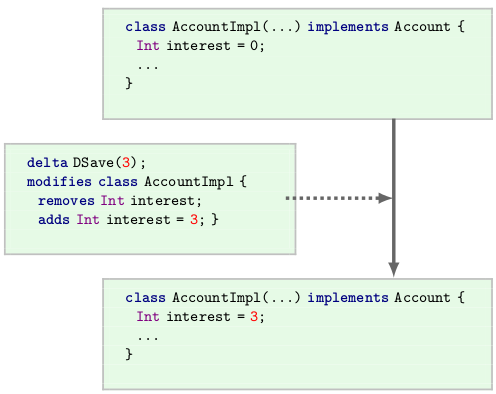
One or more features can be put into a file with extension .abs. The connection between different deltas and a base implementation is given via the uses clause that refers to the module where the base is found. Like classes, deltas can have parameters, however, these are not fields, but are instantiated at product build time. Normally, there is a correspondence between the parameters of deltas and those of the features they are supposed to implement. The modified withdraw(Int) method is implemented by a suitable call to the original version after a check that the withdrawn amount is not trivially small. We must declare a result variable to ensure that the return statement is last. Assume further we want to realize the Save feature. One must ensure that the interest rate is set to 0. ABS deltas at this time do not support to add or modify class initialization blocks. To change the initial value of a field, we simply remove the field declaration and add it again with a suitable initial value:

delta DSave(Int i); // Implements feature Save
uses Account;
modifies class AccountImpl {
   removes Int interest;
   adds Int interest = i;
}

Of course, we assume here that the interest field has been added in the first place in the earlier delta DType. This requires to specify and check temporal constraints on the application of deltas as we shall see in the following section. Application of a concrete delta is illustrated with DSave in Fig. 14. Syntax and parse error highlighting for delta modules works as usual. Automatic completion works as well, but it is only done relative to the base product.

The reason is that before product build time, the compiler cannot know which deltas have been applied before. For the same reason, only a limited amount of type checking is done. Research to lift type checking to the family level is under way [29, 37].

8.4 Product Line Configuration

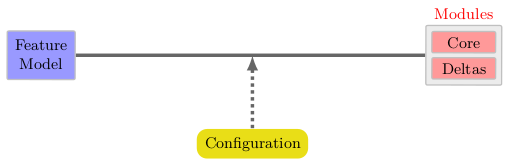
So far, we have two models relating to product lines: the feature model and the delta model, that is, the feature implementation. Unlike any other formalism we are aware of, in ABS we can make a formal connection between these. This is the key to being able to analyze whole product lines and not merely individual products. In ABS, the connection between features and their realization (illustrated in Fig. 15) is done in a dedicated product line configuration file. This makes debugging easy, because all information about the realization of a given feature model is collected in one place. To establish a connection between features and deltas, the configuration files need to specify three things:

they must associate features with their implementing delta modules by application conditions;
they need to resolve conflicts in the application order by giving partial temporal constraints on delta application;
they need to pass the attribute values of features to the parameters of the delta modules.

We can illustrate all three aspects with our running example. The following file (again, use file extension .abs) defines a product line named Accounts based on the five features of the feature model in Fig. 12.

productline Accounts;
features Type, Fee, Overdraft, Check, Save;
delta DType (Type.i) when Type;
delta DFee (Fee.amount) when Fee;
delta DOverdraft after DCheck when Overdraft;
delta DSave (Type.i) after DType when Save;
delta DCheck after DType when Check;

For each delta that is to be used for implementing any of the features one specifies:

the application conditions (when clauses), that is, the feature(s) that are being realized by each delta and whose presence triggers delta application;
the delta parameters which are derived from feature attribute values;
a strict partial order of delta application (after clauses) to ensure well-definedness of delta applications and resolve conflicts.

In the example, there is a one-to-one correspondence between deltas and features, which is reflected in the application conditions. Likewise, the feature attributes Type.i and Fee.amount directly can be used as parameters of the corresponding deltas. The temporal constraints of DSave and DCheck ensure that the field interest is present. The constraint of DOverdraft makes sure that this delta is only applied to checking accounts. It would also have been possible to express this constraint at the level of the feature model with an includes: clause. It is up to the modeler to decide whether a given constraint is a property of the feature model or of the product line.

8.5 Product Selection

The final step in PLE with ABS is product selection. Whereas the activities that took place until now can be viewed as mostly being part of family engineering, the selection process is always part of application engineering.

$The role of product line configuration in product selection and\ncompilation$ $The role of product line configuration in product selection and\ncompilation$

To create a product it is sufficient to list the features that should be realized in it and to instantiate the feature attributes with concrete values. The syntax is very simple and self-explaining. As any other ABS file, product selection files have the .abs extension and there is Eclipse support for syntax and parse error highlighting. Some examples for the Accounts product line are as follows:

product CheckingAccount (Type{i=0},Check);
product AccountWithFee (Type{i=0},Check,Fee{amount=1});
product AccountWithOverdraft (Type{i=0},Check,Overdraft);
product SavingWithOverdraft (Type{i=1},Save,Overdraft);

The simplest product that can be built is CheckingAccount. The second product above extends it by charging a fee of one unit per transaction. The ABS compiler uses the product selection file and the other related files to create a “flattened” ABS model where all deltas have been applied such that it contains only core ABS code. In a first step, the compiler checks that the product selection is valid for the given feature model as described in Sect. 8.2. It then uses the product line configuration file to decide which deltas need to be applied and how they are instantiated. The partial order on the deltas is linearized. It is up to the modeller to ensure (possibly, by adding temporal constraints) that different linearizations do not lead to conflicting results. Finally, the resulting core ABS model is type-checked and compiled to one of the ABS backends in the standard way. As all parts of the ABS language the product line modeling languages have a formal semantics—the details are found in [10]. Different products can be selected in the Run|Run Configurations ... dialog from the ABS Product menu. Invalid product selections or type errors in the configuration files will be displayed at this stage. For example, selection of the SavingWithOverdraft product above results in an error, because the constraints in the feature model are not satisfied.

After selection of a valid product one can run and debug the resulting core ABS model as described earlier. The ABS compiler additionally creates always as base product that corresponds to the given ABS model without any features or deltas. This product appears under the name <base> in the product selection menu. If we execute the main class of the Account module in Sect. 6.4 in the base product, we obtain the result 37 in the variable net, whereas if we run the product AccountWithFee, we obtain 34. A current limitation of the Eclipse ABS plugin is that the debugger correctly displays the runtime configuration and the values of variables of products, but in the editor window only the core product is displayed.

9 Concluding Remarks

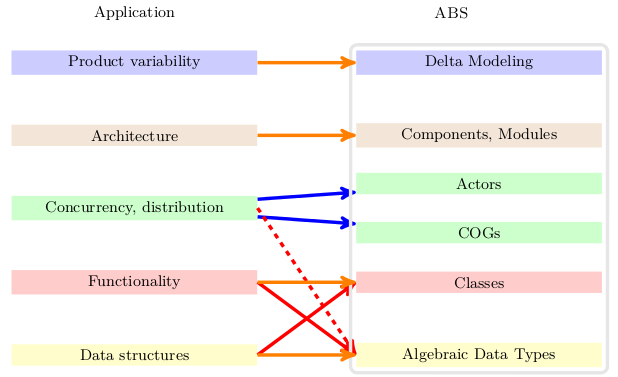
In this tutorial we gave an introduction to the abstract modeling language ABS. Uniquely among current modeling languages, ABS has a formal semantics and covers the whole spectrum from feature modeling to the generation of executable code in Java. Development of ABS models is supported by an Eclipse plugin. A very important point is that ABS offers a wide variety of modeling options in a uniform, homogeneous framework, see Fig. 17. This allows to select an appropriate modeling style for each modeled artifact. It also supports rapid prototyping and design-time analysis, because ADT-based models can be refined later (dashed arrow). Of course, as any other formalism, ABS has also limitations: it is not suitable to model low-level, thread-based concurrency with shared data. Hence, ABS is not suitable to model multi-core applications or system libraries. In this sense, approaches such as [5] are complementary to ABS. As mentioned earlier, the analysis capabilities and the ABS runtime component layer are beyond this tutorial, but some chapters in this volume cover part of the material.

Acknowledgments

The development and implementation of ABS was a collaborative effort of the many researchers involved in the HATS project. While the text of this tutorial has been written from scratch by the author, it could never have been done without the background of all the papers, presentations, and discussions provided by many colleagues. Special thanks go to the main contributors to Work Package 8: Frank de Boer, Einar Broch Johnsen, and Ina Schaefer.