Resource Modeling Tutorial

The object-oriented perspective on timed behavior is captured by deadlines to method calls. Every method activation in Real-Time ABS has an associated deadline, which decrements with the passage of time. This deadline can be accessed inside the method body with the expression deadline(). Deadlines are soft; i.e., deadline() may become negative but this does not in itself block the execution of the method. By default the deadline associated with a method activation is infinite, so in an untimed model deadlines will never be missed. Other deadlines may be introduced by means of call-site annotations. Real-Time ABS introduces two new data types into the functional sublanguage of ABS: Time, which has the constructor Time(r), and Duration, which has the constructors InfDuration and Duration(r), where r is a value of the type Rat of rational numbers. The accessor functions timeVal and durationValue return r for time and duration values Time(r) and Duration(r), respectively. Let o be an object which implements a method m. Below, we define a method n which calls m on o and specifies a deadline for this call, given as an annotation and expressed in terms of its own deadline. Remark that if its own deadline is InfDuration, then the deadline to m will also be unlimited. The function scale(d,r) multiplies a duration d by a rational number r (the definition of scale is straightforward).

Int n (T x){ [Deadline: scale(deadline(),0.9)] return o.m(x); }

In the explicit time model of Real-Time ABS, the execution time of computations is modeled using duration statements duration(e1,e2) with best- and worst-case execution times e1 and e2. These statements are inserted into the model, and capture execution time which does not depend on the system’s deployment architecture. Let f be a function defined in the functional sublanguage of ABS, which recurses through some data structure x of type T, and let size(x) be a measure of the size of this data structure x. Consider a method m which takes as input such a value x and returns the result of applying f to x. Let us assume that the time needed for this computation depends on the size of x; e.g., the computation time is between a duration 0.5*size(x) and a duration 4*size(x). An interface I which provides the method m and a class C which implements I, including the execution time for m using the explicit time model, are specified as follows:

interface I {
  Int m(T x)
}
class C implements I {
  Int m (T x){
    duration(0.5*size(x), 4*size(x)); return f(x);
  }
}

In the implicit time model of Real-Time ABS, the execution time is not specified explicitly in terms of durations, but rather observed on the executing model. This is done by comparing clock values from a global clock, which can be read by an expression now() of type Time. We specify an interface J with a method p which, given a value of type T, returns a value of type Duration, and implement p in a class D such that p measures the time needed to call the method m above, as follows:

interface J {
  Duration p (T x)
}
class D implements J (I o) {
  Duration p (T x){
    Time start; Int y;
    start = now();  y=o.m(x);
    return timeDifference(now(),start);
  }
}

Observe that by using the implicit time model, no assumptions about execution times are specified in the model above. The execution time depends on how quickly the method call is effectuated by the called object. The execution time is simply measured during execution by comparing the time before and after making the call. As a consequence, the time needed to execute a statement with the implicit time model depends on the capacity of the chosen deployment architecture and on synchronization with (slower) objects.

A deployment component in Real-Time ABS captures the execution capacity associated with a number of concurrent object groups. Deployment components are first-class citizens in Real-Time ABS, and provide a given amount of resources which are shared by their allocated objects. Deployment components may be dynamically created depending on the control flow of the ABS model or statically created in the main block of the model. We assume a deployment component environment with unlimited resources, to which the root object of a model is allocated. When objects are created, they are by default allocated to the same deployment component as their creator, but they may also be allocated to a different component. Thus, a model without explicit deployment components runs in environment, which does not impose any restrictions on the execution capacity of the model. A model may be extended with other deployment components with different processing capacities. Given the interfaces I and J and classes C and D defined in above, we can for example specify a deployment architecture in which two C objects are deployed on different deployment components server1 and server2, and interact with the D objects deployed on a deployment component clientServer. Deployment components in Real-Time ABS have the type DC and are instances of the class DeploymentComponent. This class takes as parameters a name, given as a string, and a set of restrictions on resources. The name is mainly used for monitoring purposes. Here we focus on resources reflecting the components’ processing capacity, which are specified by the constructor CPUCapacity(r), where r represents the amount of abstract processing resources available between observable points in time. Below, we create three deployment components Server1, Server2, and ClientServer, with the processing capacities 6, 3, and unlimited (i.e., ClientServer has no resource restrictions). The local variables server1, server2, and clientServer refer to these three deployment components, respectively. Objects are explicitly allocated to the servers by annotations; below, object1 is allocated to Server1, etc.

{ // This main block initializes a static deployment architecture:
  DC server1 = new DeploymentComponent("Server1",set[CPUCapacity(6)]);
  DC server2 = new DeploymentComponent("Server2",set[CPUCapacity(3)]);
  DC clientServer = new DeploymentComponent("ClientServer", EmptySet);
  [DC: server1] I object1 = new cog C;
  [DC: server2] I object2 = new cog C;
  [DC: clientServer] J client1monitor = new cog D(object1);
  [DC: clientServer] J client2monitor = new cog D(object2);
}

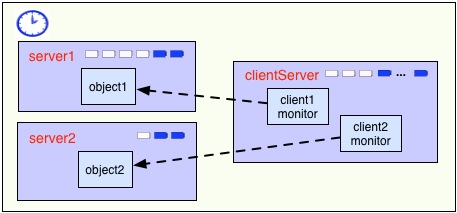
The figure depicts this deployment architecture and the artefacts introduced into the modeling language. Since all objects are allocated to a deployment component (which is environment unless overridden by an annotation), we let the expression thisDC() evaluate to the deployment component of an object. For convenience, a call to the method total("CPU") of a deployment component returns its total amount of allocated CPU resources.

class C2 implements I {
  Int m (T x){ [Cost: g(size(x))] return f(x);
  }
}

class C3 implements I {
  Int m (T x){ [Cost: size(x)*size(x)] return 0;
  }
}